椭圆中的美学与数学——以《椭圆及其标准方程》教学实践为例

选题背景

英国数学家Alfred North Whitehead提出“数学的本质不仅是逻辑，更是模式与美的科学”，强调数学结构本身具有和谐之美，而审美直觉能促进数学的创造性思维，可见数学与美学原本就具有深层联系。当下教育改革提倡“五育融合”，如何将美育渗透到数学教学中，提升学生的数学思维和审美价值是重要的研究课题。普通高中数学“圆锥曲线”包含丰富的美学元素，是展现数学美的重要载体，也是利用美学促进数学发现、激发学生数学兴趣的巧妙着力点。但目前课堂教学中，教师注重知识的教授、运算技巧的讲解，常常忽视了美学与数学的交互。

《椭圆及其标准方程》作为“圆锥曲线”教学内容的起始课，在研究策略和思想方法上起着重要的引领作用，且具有丰富的美育要素可挖掘。例如，章头语圆锥曲线的原始定义可以体现圆锥曲线的统一美，从三维空间的原始定义到二维平面的第一定义的衔接可以感悟多种定义的和谐美等。因此，本文以《椭圆及其标准方程》为例进行美育浸润的教学设计实践。

教学目标

1.经历从具体情境抽象出椭圆的过程，掌握椭圆的定义及其标准方程。

椭圆的定义有多种呈现形式，本课例根据教材主要呈现圆锥曲线的原始定义和第一定义，从三维空间中让学生感受圆锥曲线的统一性，从二维平面中让学生理解椭圆第一定义的严谨性。

2.通过绘制椭圆的过程严谨认识椭圆定义，经历方程的推导过程培养直观想象、逻辑推理、数据运算等核心素养。

通过感受—发现—验证定义，体会数学定义概念的简洁、严谨、统一，是数学中美学的体现；经历建系—设点—化简方程，用美学启发数学思维，激发创造力，落地核心素养。

3.感受并发现数学研究过程中美的呈现，对数学的内在结构和思想的理性美充满好奇与欣赏。

利用平面截圆锥的模型展示、旦德林双球模型展示以及拉线作图的实践操作，感受数学的模型美、形状美，激发学生学习的兴趣和探索的欲望。

教学设计创新

1.引入方式的创新。

本课例没有直接引入“拉线作图”情境得出椭圆定义，而是选用两个情境层层递进引出椭圆定义。一是利用章头语介绍圆锥曲线统一定义，引出“椭圆”；二是利用点光源照射球实验引出“焦点”，并借助旦德林双球模型展示二维平面椭圆上的点与两个焦点之间的关系。这一设计实现了椭圆定义从三维空间到二维平面的平稳过渡，使学生的认知理解更加自然和顺畅。

2.美学引领问题串的推导方式创新。

课例中并未采用以教师为主导的方式进行方程的推导，而是通过学生小组合作的形式，配套具有指引性的问题串引导学生进行方程化简，发现数学的对称美、简洁美。

3.丰富动态展示的技术创新。

课例多处设置了动态模型、动手实验，旨在提升学生学习兴趣的同时，借助动态生成的过程激发学生的创造力，引导学生体悟感性美到理性美的升华。

教学实施

1.立足全章，构建定义—感受形状美、模型美

师：圆锥曲线的名称由何而来？它与圆锥有什么联系？

情境1：GGB动态展示平面截圆锥模型（见图1）

师：用一个垂直于圆锥的轴的平面截圆锥，截口曲线是一个圆，如果改变圆锥的轴与平面形成的角，会得到怎样的曲线？

图1

【师生互动】用不垂直于圆锥曲线的轴的平面截圆锥，直观观察得到不同曲线，有椭圆、双曲线、抛物线，统称为圆锥曲线，引导学生理解曲线名称的来源和三种曲线之间必然存在的紧密联系。

师：在之前直线与圆的学习研究中，我们体会了坐标法研究几何的魅力与威力，现在延续这种思路，继续研究椭圆。

情境2：生活实验模拟旦德林双球模型

【师生互动】教师用手电筒照射桌面放置的乒乓球，学生观察球的影子形状。当光线垂直于桌面，影子为圆形；当光线斜射小球时，影子为椭圆形。影子为圆形时，圆心就是球与桌面的切点，影子边缘上的点到切点距离不变，是圆的定义。启发学生思考影子为椭圆形时，此时的切点到影子边缘的距离是否不变。

师：当影子为椭圆形时，切点在一边，这个切点位置是做不到距离不变的。1个切点办不到，猜测可能会有几个？

【模型介绍】光线是无限延展的，延展开的光线是一个圆锥，小球是与圆锥内切，桌面相当于一个平面截圆锥且与小球相切，事实上，下方也有一个大的球与圆锥和平面同时相切。这个模型就是著名的旦德林双球模型，这里呈现的两个切点就是椭圆的关键要素“焦点”（见图2）。

图2

师：两个焦点与椭圆上的点有什么量化关系？

【师生互动】教师拖动P点运动，引导学生发现距离之和不变。数据度量直接证明椭圆上的点到两个焦点的距离之和为定值，教师可从几何角度简单说明定值的原因。

2.归纳定义，推导方程—发现严谨美、简洁美

活动1：拉线作图验证第一定义

师：椭圆上的点到两个焦点的距离之和为定值，反过来，若满足到两定点距离之和为定值，点的轨迹一定是椭圆吗？接下来自己动手验证，请按照教材的探究画一画。

【师生互动】教师引导学生在白纸上用钉子固定两个点，并用一个绳子连接，进行拉线作图（见上页图3），然后改变两个点的距离，研究观察。

师：在作图过程中，什么时候轨迹是椭圆？线段关系如何？

图3

生：三个点可以形成三角形时，要满足PF1+PF2>F1F2。

师：改变两点间距离后发现了什么？

生：当两点间距离和绳子长度一样时，轨迹就是线段F1F2；当距离超过绳子长度时就画不出来，不存在。

【定义析出】平面内到两个定点F1F2的距离和等于常数2a（2a>|F1F2|）的点的轨迹叫作椭圆。

活动2：小组合作推导椭圆方程

师：请小组合作，根据以下几个问题，通过坐标法探索椭圆的方程。

问题1：如何用数学符号语言严谨刻画椭圆的定义？

问题2：如何建立恰当的直角坐标系，使设点更加合理？

问题3：如何化简方程，使方程便于记忆，称之为“标准方程”？

【师生互动】利用定义，学生很快得出符号语言的表述：PF1+PF2=2a（2a>F1F2）。追求简洁性与对称性，一般以F1F2为x轴，线段F1F2的中点为原点建立直角坐标系，设点P（x，y），F1（-c，0）F2（c，0），利用两点间距离公式，得出方程：

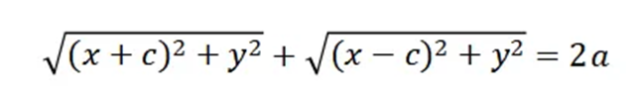
此时的方程不具有美观性和可记忆性，启发学生通过移项、平方、化简寻求简洁美，得到

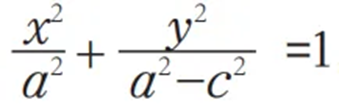
但式子结构不具备对称美，继续优化引入b，

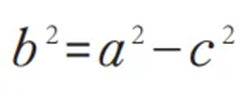
并利用关系找到b在几何图形中的位置，最终得出

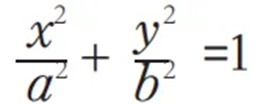
3.回顾反思，提炼升华—欣赏过程美、方法美

师：本节课学习了椭圆的定义及其标准方程，回顾是如何一步步探究的？

生：通过平面截圆锥发现圆锥曲线的存在，找到椭圆；旦德林双球模型引出焦点发现了椭圆上的点与两个焦点的距离之和为定值，拉线作图严谨验证椭圆轨迹形成的条件，得出椭圆的第一定义，最后通过坐标法得出标准方程。

师：通过数学的视角，我们在椭圆形中感受到哪些美学瞬间？

生：椭圆的形状具有对称美，方程有简洁美和对称美，圆锥曲线的原始定义具有统一美，椭圆的第一定义具有严谨美……

【PPT呈现】（见图4）

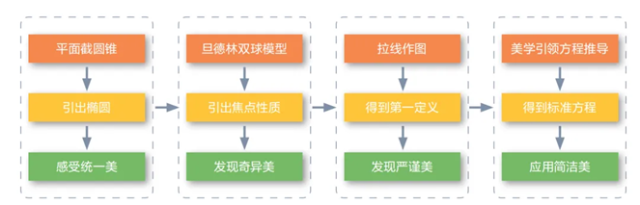
图4

4.及时巩固，熟练应用—拓展思维美、应用美

教师可通过以下例题帮助学生及时练习并巩固所学知识。

例1：已知椭圆经过点

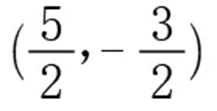
且它的两个焦点坐标分别为（-2，0），（2，0），求它的标准方程？

例2：如果椭圆

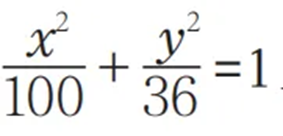
上的一点P与焦点F1的距离为6，那点P与另一个焦点F2的距离是多长？

（李婷 作者单位系浙江省长兴县太湖高级中学）

《人民教育》2025年第15-16期，原文有修改